Using Outside Angles
You may occasionally need to use an angle outside of a triangle to find an angle inside that triangle. Because a straight line can also be described as a straight angle that measures 180°, you can find the measure of any inside angle if you know the outside angle.

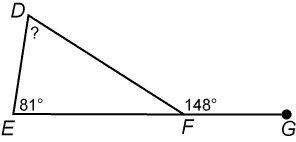
For example, you have a triangle labeled EDF that sits on line segment EFG. E and the F are points on the line and also vertexes of the triangle. The D is the top vertex of the triangle and G is the furthest point on line EFG. You know two things about triangle EDF - that ∠DEF is 81 degrees and the the outside angle of vertex F, ∠DFG, is 148 degrees. That is enough information to find all three angles of triangle EDF.
Step 1: Subtract 148° from 180° to find the measure of \(\angle EFD\)
\(180^\circ -148^\circ = 32^\circ \)
Step 2: Find the sum of the known angles.
\(81^\circ + 32^\circ = 113^\circ\)
Step 3: Subtract 113° from 180° to find the unknown angle.
\(180^\circ -113^\circ = 67^\circ\)
Answer: The measure of \(\angle EDF\) is 67°.